引 言

当城市道路上发生紧急事故时，应急救援车辆需要获得时空路权上的优先，以进行快速救援。近年来随着智能网联技术的发展，交通路网复杂的时变信息得以被准确估计并通过网联进行通信交互，这使得应急车辆动态的时空路权优化成为可能[1-2]。

值得注意的是，针对应急救援车辆的时空路权优化研究主要在信号绝对优先(时间权)的前提[3]下对救援路径(空间权)进行规划。目前动态路径优先算法可以分为两类：阶段式全局调整方法与局部路径动态调整方法。其中阶段式全局调整方法是在应急车辆运行过程中利用如A*[4]、遗传算法[5]等启发式算法针对路网静态指标进行全局路径规划更新，但由于路网具有动态不确定性，且启发式算法计算效率较低，易得到陷入局部最优，无法满足实时性要求。局部路径动态调整方法则是利用实时获取的动态信息，剔除路网的部分较劣的路径与节点进行车辆的局部路径规划[6-7]。该方法通常计算复杂度较低，计算速度快，更适合应急车辆的动态路径优先任务。也有研究考虑了应急信号绝对优先对于路网整体的负面影响[8-10]，从而给予应急车辆相对信号优先以减少对于路网的负面影响。

然而，目前针对应急车辆时空路权优化的研究都是在首先确定时间路权(绝对或相对优先)的前提下进行空间路权规划，难以有效针对路网的动态变化同步调整应急车辆的路径与应急优先信号，从而导致应急救援和路网运行效率难以达到预期。因此，迫切需要建立一种适用于应急车辆的时空路权同步动态优先方法。模型预测控制(Model Predictive Control, MPC)是一种通过系统当前的输入与预测范围滚动变化进行系统后续状态预测与控制优化的方法[11]，其通常将控制目标转化为二次规划问题进行可行解求解，具有计算效率快，控制过程动态可调整等优点，可以满足应急车辆运行过程中的多参数动态调整要求。

基于以上背景，本研究考虑应急信号优先对路网的影响，引入了路网韧性指标，建立了双层MPC应急车辆路径选择控制器，以实现应急车辆时空路权同步动态优化。

1 路网韧性指标与模型预测控制

1.1 背景假设

针对智能网联环境下的应急车辆时空路权动态优化，本研究进行如下假设：

(1)路网中仅有单方向上的应急车辆需进行应急信号优先控制，无多应急信号优先冲突产生；

(2)假设所有道路均为双向单行道，应急车辆及社会车辆均无换道行为产生。

1.2 路网韧性指标

由于不同的交通流运行状况会对路网供给能力产生很大的影响，本研究在基于传统网络拓扑特征构建的有效性指标基础上，结合行程时间作为网络的边权值，构建考虑路网交通流动态特征的网络。选择路段长度及服务水平构建边权重计算公式如下[12]

(1)

式中 Wi表示路段i的权重；Li表示路段i总长度；qi表示路段i的交通量；ci表示路段i的通行能力。道路的通行能力在交通供给上意味着单位时间内不同的交通供给能力，即一定条件下城市路网单位时间内能够容纳的最大车辆数，是度量路网疏导车辆能力的一项重要指标。路段和交叉口是构成城市道路网络的基本环节，而这两个环节失效是降低城市道路网络韧性能力的最直观原因。传统的道路网络韧性能力研究通常构造有效性指标来计算路网的脆弱程度，有效性指标E用于衡量信息在网络节点间传递的效率

(2)

式中 N表示路网中交叉口数量。有效性指标E为路网韧性指标，其值越高，表示网络的连通效果越好，当路网中某部分出现故障时维持路网正常运转的能力越强。本文利用将路网有效性结合应急车辆运行效率作为车辆路径选择的参考指标，进行车辆路径选择的多目标动态优化。

1.3 模型预测控制(MPC)原理

模型预测控制构架的主体是由预测模型、反馈校正、滚动优化等部分组成，其中心思想是利用预测范围的滚动对模型进行实时的反馈，并不断调整输出结果。以应急车辆为例，模型预测控制下车辆可以根据实时接收当前预测范围内的各类网联信息(如车辆状态、交通流等)，并与预测值进行对比，以此作为反馈来调整模型的输出(如车辆的控制参数、路径选择等)，并不断滚动重复，从而达到动态调整优化的目的。原理如图1所示。

图1 应急车辆模型预测控制原理示意图

2 双层MPC应急车辆路径选择控制器设计

为实现应急车辆的时空路权动态优化，本文采用如图2所示的双层MPC应急车辆路径选择控制器，通过路径规划层与车辆控制层的应急车辆行驶预测结果，提供车辆行驶路径上交叉口的应急信号优先，并动态计算应急车辆行驶过程中所属相位的信号绿灯时长。

图2 双层MPC应急车辆路径选择控制器示意图

2.1 车辆控制器设计

智能网联环境中的应急车辆需根据网联信息进行实时道路交通预测以及动态轨迹控制，以实现应急车辆的精准操纵并提高其运行效率与安全性。为符合车辆运行特征，动态预测非应急车辆的车辆运行状态，并对其他车辆的驾驶行为进行预测，下层控制器采用车辆动力学形式的模型预测控制。根据车辆动力学原理，车辆的运行状态如下：

Vt+1=Vt+atb

(3)

(4)

式中 b表示采样间隔时间，即为预测步长；Xt表示t时刻的车辆位置；Xt+1表示t+1时刻的车辆位置；at表示t时刻的车辆加速度；Vt表示t时刻的车辆速度；则应急车辆在t时刻的运行状态空间方程表示为

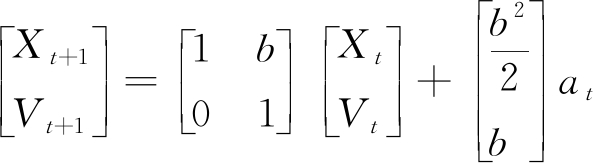
(5)

因此应急车辆的加速度为控制变量，其位置与速度为状态变量。由于应急救援任务的时效性，对于应急车辆的控制过程仅考虑车辆运行的效率，因此应急车辆的目标函数可设为如下式所示的硬约束模型预测控制

(6)

式中 t0表示车辆运行预测的初始时刻，且在实验中假设应急车辆的初始速度即接近自由流速度，在此目标下期望应急车辆可以维持此速度到达目标地点。制定属于当前道路场景的约束，包括：位置约束Pr+1≤Xtε，速度约束0≤Vt≤Vfree,Vfree表示自由流速度，加速度约束amin≤at≤amax,amax表示最大加速度，amin表示最小加速度。将预测范围内所有预测时刻的状态变量与控制变量at合并为变量y′，表示为

y′=[Xt0 Vt0 Xt0+b Vt0+b … Xt0+b×c Vt0+b×c

at0 … at0+b×c-b]

(7)

式中 c表示预测次数，其值为预测范围与采样时间间隔的除数取整。利用变量y′将上述约束与应急车辆空间状态转换为如下二次规划问题

(8)

其中，H′的值为：

(9)

h′∈R(2c+2)×(2c+2)

的值为

的值为：

yy′=[NA, Vfree, …, NA, Vfree]T,yy′∈R1×(2c+2)

式中 NA表示正无穷，Vfree表示道路自由流速度；矩阵Aeq′的值为：

A′∈R2c×(2c+2)

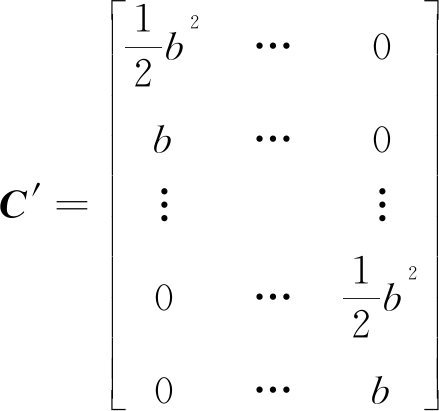
矩阵beq′的值为

同时根据交叉口信号配时与非应急车辆的行驶特点，利用模型预测控制进行普通车辆的运行状态预测。根据智能网联环境下的通信信息，可实时预测非应急车辆的运行状态，对于非应急车辆，其运行过程中的目标函数设为如下式所示的软约束模型预测控制

(at-at+1)2]

(10)

其表示非应急车辆在考虑安全、效率以及排放等多运行目标的前提下，预测社会车辆的行驶方式。通过二次规划可解得非应急车辆的运行状态可行解，并将此可行解视为对非应急车辆运行状态的预测结果。

2.2 路径选择器设计与应急信号优先方案

当实际路网被抽象为邻接矩阵后，通过A*算法[13]获得车辆的初始路径，并将路径中所有交叉口与应急车辆的出发地与目的地视为应急救援路径的节点。通过如图3所示的应急路径选择流程，对于应急车辆的行驶路径进行动态调整。其中在应急车辆的模型预测控制过程中，首先以车辆通过选择路径时间最短为目的，设定应急车辆运动过程的目标函数为

图3 路径选择逻辑流程图

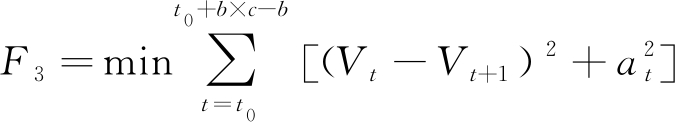
(11)

该目标函数表明期望应急车辆在行驶过程中考虑自身制动性能的前提下对以最高效率通过当前路段。由于该目标函数中加速度为硬约束，则应急车辆的加速度受约束条件影响，从而可利用模型预测控制及二次规划计算出应急车辆最短可通过所选部分路径的时间后，综合路网韧性指标，最终通过下式计算得到所有备选路径的应急衡量指标F

F=0.8Tj-0.2Ej

(12)

式中 Tj表示预测应急车辆通过j条路径的时间，Ej表示当应急车辆行驶于路径j上的路网韧性指标，最终将应急衡量指标计算值最小的路径k视为最优路径。应急车辆在每次通过当前交叉口并进入下一路段后重新开启路径选择器进行下一路段的路径选择，并对所选择路径的交叉口发送应急信号优先的指令。

当交叉口收到应急信号优先指令后，即刻将应急相位调整为绿灯，通过路径选择器预估的应急车辆通过路段时长给予应急相位绿灯时长。由于实际道路车辆的动态变化以及车辆控制过程中可能带来的时延，通过车辆控制器的应急车辆通行时间结果不断对应急相位绿灯时长给予调整。

3 仿真结果与分析

本文利用Matlab仿真软件进行仿真模拟实验，路网中不同类型车辆的实验参数取值如表1所示。实验采用江苏省昆山市部分路网作为背景，该部分路网如图4所示，其以昆山南站为中心，包含附近主要枢纽及公共场所。

表1 不同车辆实验参数

图4 昆山市部分路网拓扑图

在此拓扑路网上，进行应急车辆仿真模拟实验，结果如图5所示。在A*算法下，应急车辆可找到路网中的最短路径，但由于车流量以及应急信号优先策略的影响，考虑应急车辆运行效率以及路网韧性时，应急车辆的路径会发生改变。

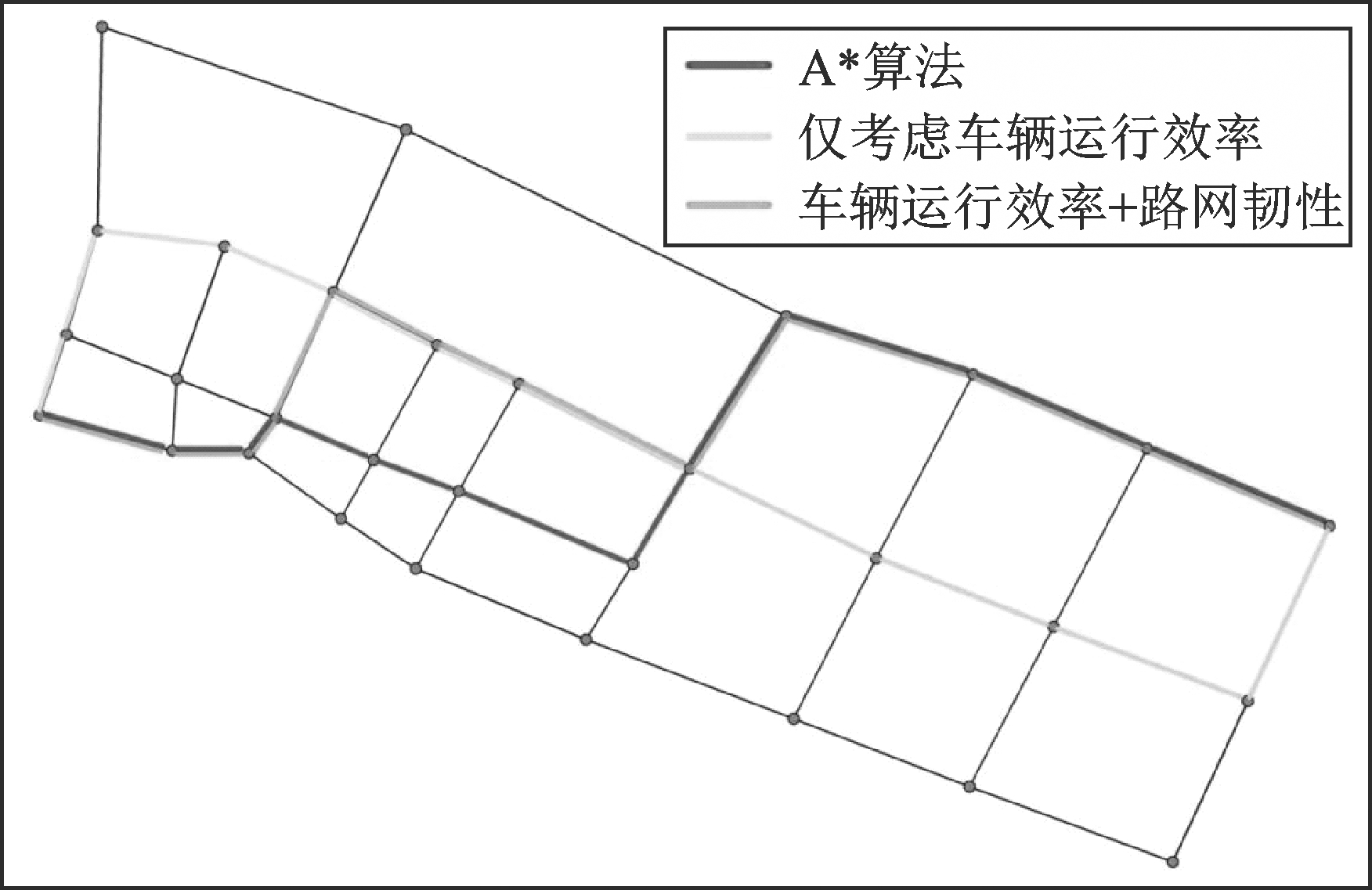
图5 不同算法下应急车辆路径选择结果

为验证不同流量下本模型的有效性，在此路网的基础上，分别设置路网中路段在不同流量密度下的应急车辆时空路权动态优化仿真实验，实验结果如表2所示。其中路段密度表示在应急车辆进入路段前，路段中非应急车辆的分布密度情况，且这些车辆在路段中的位置呈高斯分布。延迟时间计算如下

表2 不同流量下应急车辆仿真实验结果

式所示

(13)

式中 Tdelay表示应急车辆的延迟时间，∑Ti表示所有路段上应急车辆行驶的时间之和，∑Li表示应急车辆行驶的所有路段的长度之和。假设路网中所有交叉口的应急车辆行驶相位的信号周期为60 s，其中绿灯信号时长为30 s。对比有应急信号优先与无应急信号优先情况下车辆行程总时间，可知使用本文所提出的应急车辆时空路权优化方法可以有效降低应急车辆行驶延误，节约应急车辆行程时间。

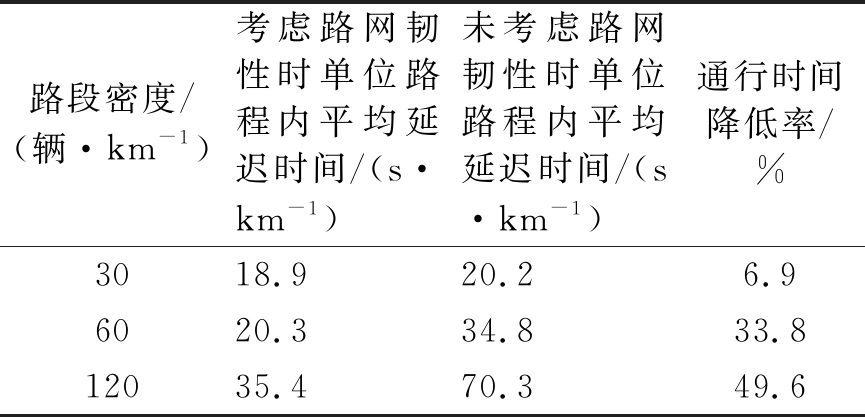
表3展示在不同流量下，应急车辆路径选择过程中是否考虑路网韧性对于非应急车辆的影响。结果表明，当应急车辆路径选择过程中考虑路网韧性时，可以有效提升其他非应急车辆的通行效率。当路段中车辆密度较低时，道路间连通度高，路网韧性较强，此时应急信号优先策略对于其他车辆的通行效率影响较低；随着路段中车辆密度的增加，本文所提出的应急车辆时空路权优化策略对于非应急车辆的通行负面效率影响显著降低。

表3 不同流量下路网韧性指标对路网的影响

4 结 论

本文根据车辆运动学模型设计了双层MPC应急车辆路径选择控制器，通过Matlab仿真平台验证了智能网联环境下在江苏省某城市部分路网中，路径选择控制器对于应急救援车辆的时空路权动态优化控制有良好的效果。得到的主要结论如下：

(1)本文提出的上层路径选择+信号优先同步优化方法对于不同道路流量下的应急路径规划有很强的适应性，特别高流量时，相比只进行路径选择的方法，应急车辆行程时间显著缩短；

(2)本文提出的优化策略能够有效降低由于应急车辆时空路权优先对路网通行效率的负面影响，同时显著提高应急救援效率。

参考文献：

[1] 吕 伟, 李志红, 马亚萍,等. 考虑受灾点需求时间窗的应急物资配送车辆路径规划研究[J]. 中国安全生产科学技术, 2020, 16(3):5-11.

[2] 姚 佼, 邵楚薇, 王品乘,等. 城市路网应急车辆路径选择模型研究[J]. 物流科技, 2020, 43(4):83-87.

[3] Cao M ,Shuai Q ,Li V . Emergency vehicle-centered traffic signal control in intelligent transportation systems[C]. 2019 IEEE Intelligent Transportation Systems Conference (ITSC), 2019: 19193793.

[4] 乔 梁, 黄加翼, 李云霄. 基于A*算法城市应急救援最优路径决策[J]. 安防科技, 2011, (3):8-10.

[5] 宋英华, 尹思杨, 杜丽敬. 基于加权遗传算法的双目标应急物资配送车辆路径优化决策模型[J]. 安全与环境工程, 2020, 27(3):86-93.

[6] Zhang X,Yu X,Wu X . Exponential rank differential evolution algorithm for disaster emergency vehicle path planning[J]. IEEE Access, 2021, 9:10880-10892.

[7] 张艺还. 车路协同环境下突发事件救援车辆路径规划算法研究[D]. 北京：北京交通大学,2019.

[8] 段晓红, 吴家新, 周芷晴. 基于层次蝙蝠算法的应急车辆调度与交通疏散协同决策[J]. 交通运输系统工程与信息, 2020, 20(2):157-165.

[9] 豆雪珊. 应急车辆交叉口优先通行辅助方法及协调控制策略研究[D]. 长春：吉林大学，2018.

[10] 龙文民, 褚端峰, 施 辉,等. 车路协同环境下紧急车辆优先通行方法研究[J]. 中国安全科学学报, 2015, 25(7):141-146.

[11] Chen S P,Xiong G M ,Chen H Y , et al. MPC-based path tracking with PID speed control for high-speed autonomous vehicles considering time-optimal travel[J]. Journal of Central South University, 2020, 27(12):3702-3720.

[12] 张树德. 基于复杂网络理论的城市道路网络脆弱性研究[D]. 哈尔滨：哈尔滨工业大学, 2014.

[13] 张海涛, 程荫杭. 基于A*算法的全局路径搜索[J]. 微计算机信息, 2007，23(17):238-239.

Dynamic optimization of road rights for intelligent networked emergency vehicles

DAI Yulu, XU Sixuan, WANG Chen， CHEN Jun

( Department of Transportation, Southeast University, Nanjing 211189, China)

Abstract： In the intelligent connected environment, the perception and interaction of accurate traffic information provides the possibility for the optimization of the dynamic time and space rights of way for emergency rescue vehicles. However, there is a lack of effective speed guidance and dynamic path planning algorithms for emergency vehicles. Therefore, using a road network in a city in Jiangsu Province as the example, we designed a dynamic right-to-way optimization method for emergency vehicle based on two-layer model predictive control (MPC). On the path planning layer, considering both emergency rescue efficiency and roadway network resilience, a MPC path planner was designed to adjust the dynamic path and provide reasonable emergency signal priority timing; on the vehicle control layer, a MPC vehicle controller was designed to generate the optimal speed solution for emergency vehicles that satisfied vehicle dynamics constraints. The results showed that the strategy proposed in this paper can effectively reduce negative impact on the traffic efficiency of the road network and significantly improve the efficiency of emergency rescue.

Key words：intelligent connected environment; road network resilience; model predictive control; emergency path planning

中图分类号：U491

文献标志码：A

文章编号:2097-017X(2021)01-0046-06

*收稿日期： 2021-06-10

资助项目： 国家自然科学基金面上项目(71971061)

第一作者简介： 戴宇露(1997-),女，博士。研究方向:智能网联交通系统。