世界各国大力发展自动驾驶技术,大规模推进测试复杂的多类交通场景,但安全风险尚未完全得到有效的防控[1]。如2018年3月18日,亚利桑那州发生了全球首例自动驾驶汽车撞死行人的严重事故[1-2]。对比分析自动驾驶路测与人工驾驶事故致因影响,是明晰自动驾驶路测事故机理,进而有效防控自动驾驶路测安全风险的重要前提。
已有的道路交通事故致因影响程度分析研究,主要针对人工驾驶。在研究对象方面,主要考虑五大类因素:生理因素[3-8]、心理因素[3-4, 6-8]等交通参与者因素;车辆性能[4, 6-7]、载重[5, 7, 9]等车辆因素;道路线形[4-7, 10-11]、标志标线[4, 6-7, 11]、车道数[6-7, 11]等道路设施因素;天气[3-7, 10-11]、光照[3, 6-7, 11]等气候环境因素;流量[3-6, 8, 10]、车速[4-7, 9]等动态交通因素。交通事故是由多影响因素耦合作用下的结果,各影响因素间存在相关性,且表现出明显的层次性[12]。在研究方法方面,道路交通事故致因影响程度分析的研究方法正逐渐从频率分析[13-14]和χ2检验[15]等基于集计模型的描述性统计,到泊松回归模型[16-17]、负二项回归模型[18-19]和Logistic回归模型[20]等基于非集计模型的多变量分析。然而非集计模型在分析过程中往往假设各影响因素之间是独立的,因此需要分析各因素综合作用下的事故致因影响程度。而相比于其他方法,贝叶斯网络是人工智能领域表达系统不确定性分析和概率推理的有效方法之一[21]。它可以利用模型中基于局部条件的依赖关系进行双向不确定性探索,以进行预测,分类和诊断分析。贝叶斯网络能够实现先验、后验信息的融合,在后验信息数据有限的情况下保证结果的稳定性,系统全面地分析各影响因素的耦合作用对交通事故的影响[22]。
中国官方尚未有自动驾驶事故数据。美国加州机动车管理局(DMV)已经建成了自动驾驶汽车运行事故报告数据库,记录了美国加州2014年以来开放的所有事故报告[23],包含制造商信息、事故信息、参与者信息、伤亡损失信息、事故细节信息和证明共六个部分。以此数据为基础,研究人员采取了文本分析[24]、描述性统计[24-26]、决策树[24]、logistic回归[25]、贝叶斯方法[23,27]等,对美国自动驾驶路测事故的基本信息进行了诸如生产厂商、严重程度、事故类型等频率统计,并对事故的影响因素进行了分析。
现有研究虽然探究了汽车碰撞前的行为、天气、碰撞时间、碰撞位置等致因影响,但缺乏针对车道数、交叉口、隔离带等道路固有属性的分析,也未能开展自动驾驶路测和人工驾驶情况的对比分析。为此,针对自动驾驶事故致因的多因素耦合特征,以及事故样本量少的局限性,本文通过构建贝叶斯网络,以道路设施、环境、交通这三大类在道路风险评估中常用的因素作为分析对象,基于美国自动驾驶汽车运行事故报告数据及关键道路设施信息,对自动驾驶路测事故进行致因影响程度分析,并与人工驾驶进行对比分析。
贝叶斯网络是一种概率网络,是基于概率推理的图形化网络[28]。贝叶斯定理是贝叶斯网络的理论基础,其核心是应用证据信息(已知样本)对有关概率分布的主观判断(先验概率)进行修正[6]。贝叶斯网络既可以进行因果推理,计算在给定原因下的后果概率,也可以进行诊断推理,计算在给定结果的情况下,各原因出现的概率[28]。
贝叶斯网络由节点、节点间的有向连线和条件概率表CPT(Conditional Probability Table, CPT)三个部分组成。其中节点表示随机变量,有向连线表示随机变量之间的因果关系,条件概率表表示变量之间的关联强度或置信度[5]。贝叶斯网络的建立,主要分为两个步骤:①建立贝叶斯网络结构,确定节点、节点之间的有向连线;②学习网络参数,确定CPT。
1.2.1 网络结构建立方法总结
贝叶斯网络的结构确定有以下三种方法[12]:
①基于专家知识和先验知识,确定贝叶斯网络的变量节点,从而确定贝叶斯网络的结构。
②通过学习样本数据,使用机器学习算法自动获得贝叶斯网络的结构。
③基于专家知识和对数据的机器学习结果,使用数据融合方法获得贝叶斯网络的结构。
自动驾驶路测可获取的事故信息尚且较匮乏,没有足够的数据能够用于贝叶斯网络结构的学习,故本文基于专家知识和先验经验建立网络结构。
1.2.2 父节点分离方法
对子节点友好的父节点分离方法(Child friendly Parent Divorcing, CfPD),是一种用于提升网络结构有效性的方法[29]。该方法通过引入一个新节点作为中间节点,将具有相似属性的节点组合在一起,可以减少所选节点传入边的数量,从而显著减小条件概率表(CPT)的大小,进而提高网络的效率,适用于较大的网络[30]。图1为父节点分离方法的示例,分析其网络效率的提升[31]。左侧的网络,节点p的CPT行数为2m,插入节点x后,右图中节点p的CPT行数为2k+1<2m。
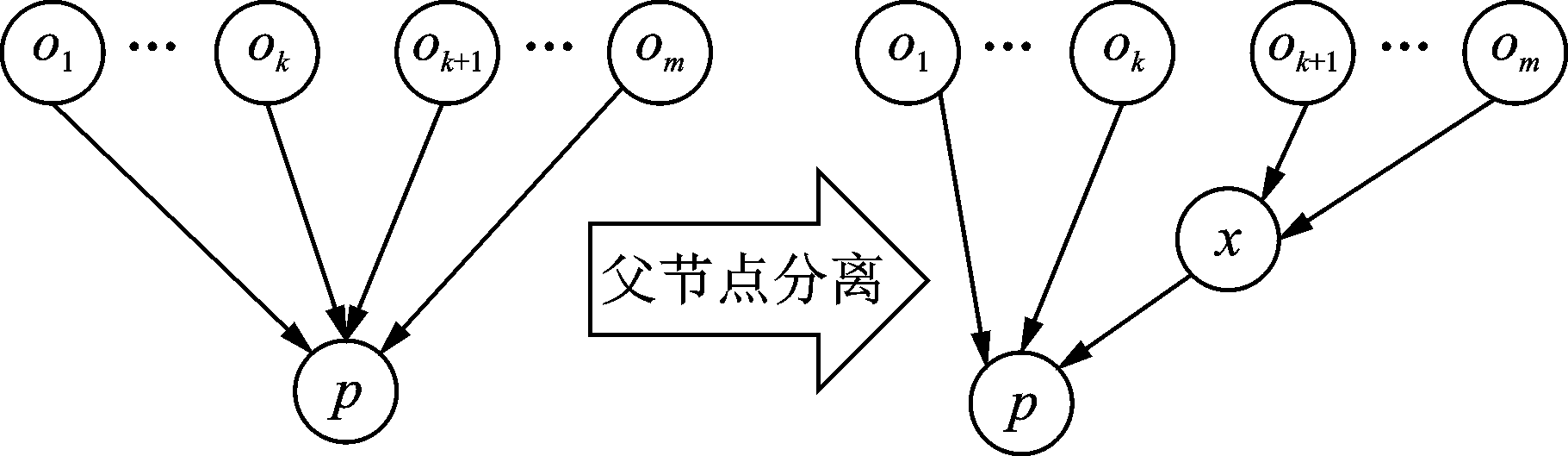
图1 父节点分离方法示例
交通事故受到众多因素耦合影响,为了尽可能全面解析事故致因,网络中包含节点的数量规模较为庞大,因此需要应用父节点分离方法,减小条件概率表(CPT)的大小,提高网络的效率。
1.2.3 分层分类的网络结构建立方法
确定贝叶斯网络结构主要分为两步:①确定网络的节点集,即确定网络中包含的变量及变量取值;②确定网络中有向边的集合,即确定变量间的相互依赖关系。
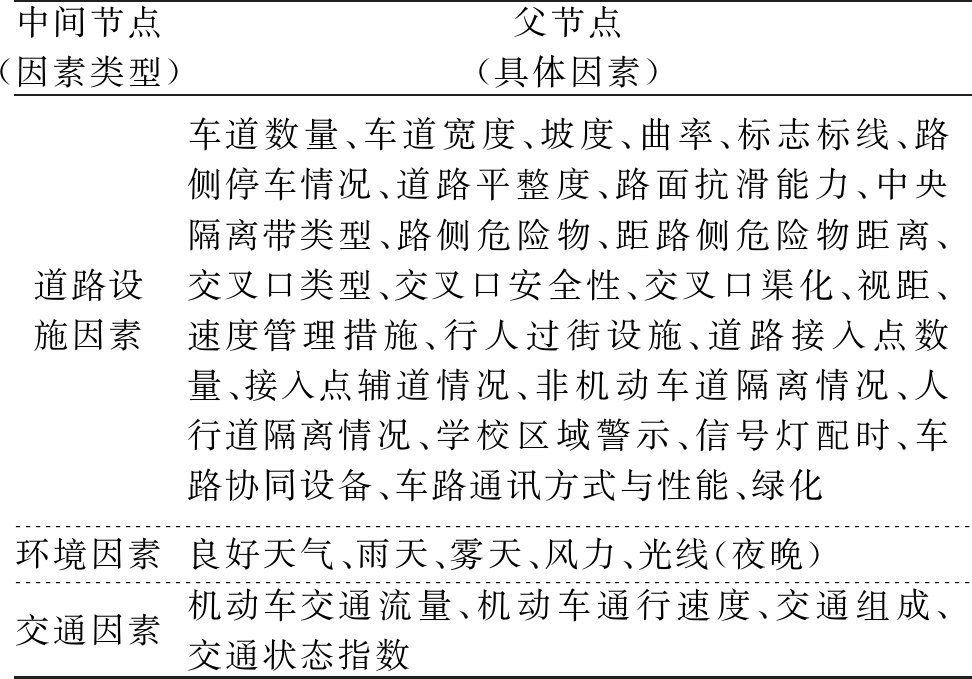
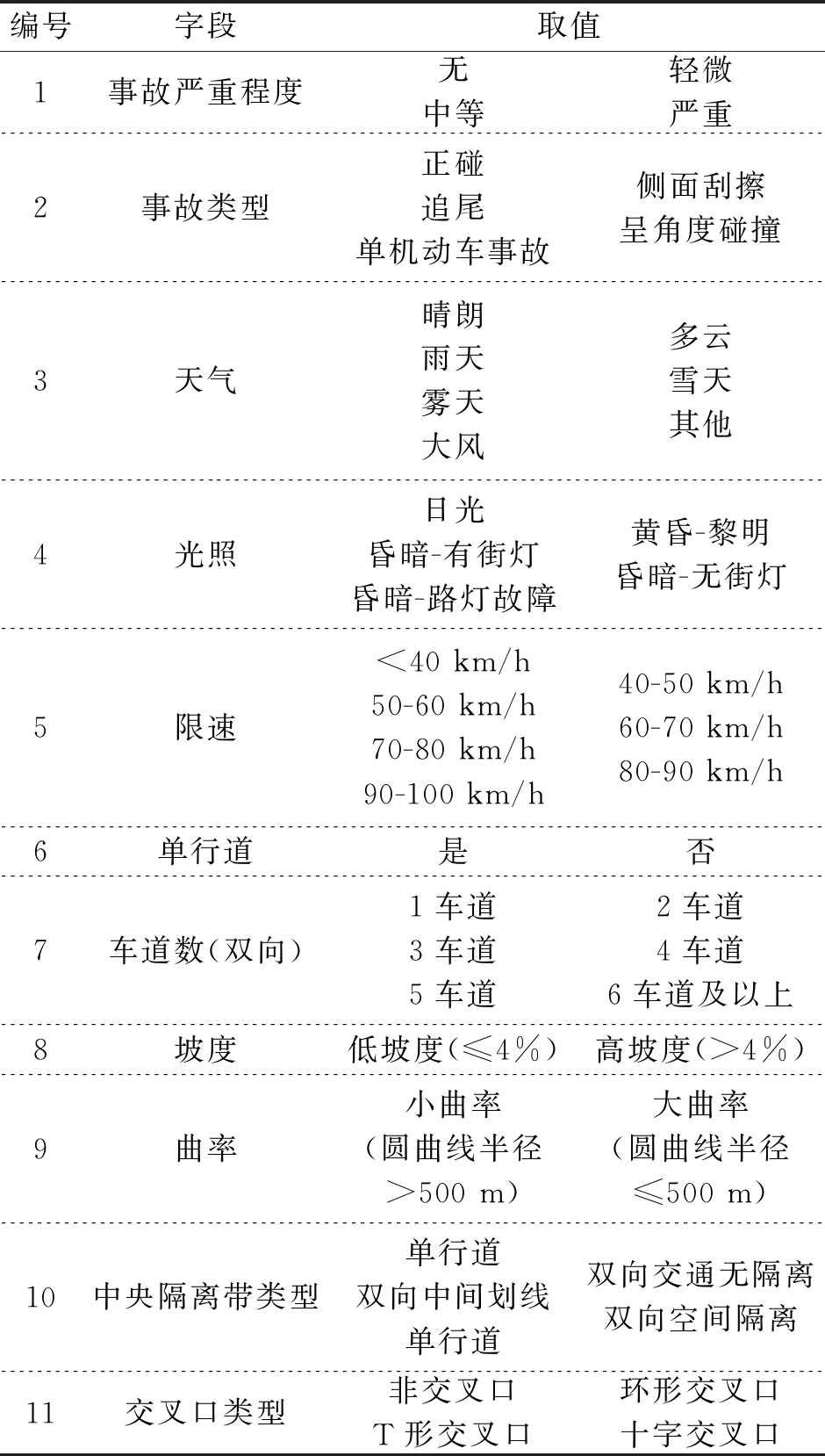
首先考虑网络的节点集。节点集包括解释变量集合和CfPD方法所引入的中间节点集合。因为CfPD方法需要聚合具有相似属性的节点,故结合自动驾驶路测的特点,对自动驾驶路测事故的影响因素进行梳理。从道路设施环境的角度考虑,主要的影响因素可分为道路设施因素、环境因素和交通因素三大类,可作为中间节点;具体共包括35个因素,可作为各中间节点的父节点,具体如表1所示。这些因素表征的是某一条具体路段具有的特征,分析这些因素对事故的影响程度,可以服务于测试路段风险度的确定。
表1 自动驾驶路测事故影响因素
基于上述影响因素梳理结果,可将网络分为三层,即事故特征层、因素类型层和具体因素层,并根据影响因素的种类分为设施、环境、交通三大类。在实际分析中根据可得数据的情况,筛选关键的因素类型,并在具体因素层筛选部分的关键影响因素作为节点。
其次考虑网络中有向边的集合。有向边在层间由具体影响因素节点,传入至影响因素类型的中间节点,最终传入至表征事故特征的节点。此外,在具体影响因素层内,还需补充各因素间的因果关系,在数据量不足的情况下,需要基于专家知识,根据可得数据中所包含的具体变量,进行相应的分析。
在贝叶斯网络结构已确定的基础上,对网络的参数进行学习。在道路事故信息的收集过程中,常会出现数据缺失的情况。大部分统计模型不能直接分析带有缺失值的数据,为确保统计模型拟合的正确性,通常都是直接删除带有缺失值的数据。进行多变量分析时,研究的变量较多,直接删除带有缺失值的数据就会消除更多的记录,可能会导致信息丢失,降低测试的效果,并使研究结果出现一些偏差[31]。
自动驾驶路测事故的数量十分有限,需要尽可能地充分利用现有信息。对于小样本下网络参数,可以融合先验信息[32],并利用最大期望(Expectation-Maximization,EM)算法进行确定。
EM算法,在数据有所缺失的情况下,针对未知参数的渐进确定性估计方法,是一个训练学习算法[33]。该方法可以基于不完整的事故数据集,计算出事故发生的条件下,各致因的各属性出现的概率值θ,从而确定CPT。EM算法主要包括两个步骤:期望步骤(也称E-Step,即Expectation Step)和最大化步骤(也称M-Step,即Maximization Step)。本文EM算法的输入为自动驾驶路测和人工驾驶的事故数据,输出为网络中各节点的条件概率表中的值。
算法的参数如表2所示。
表2 EM算法参数

算法的流程如下[34-35]:
(1)设定待估参数的初始值θ(0),算法精确度ε,以及待估参数估计值![]() 的校正值
的校正值![]()
若![]() 令
令![]()
(1)
(2)E-Step,计算事故数据集中缺失值e*的期望充分统计量
e*的概率分布为
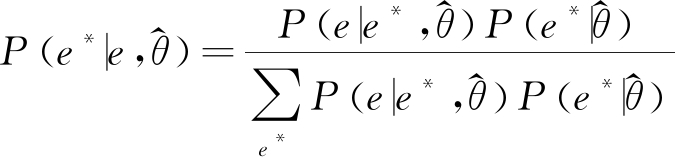
(2)
其中:

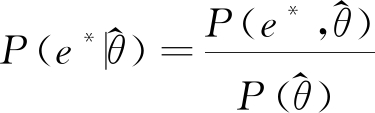
(3)
e*的充分统计量为
(4)
式中![]() 为e在e*和
为e在e*和![]() 已知条件下的概率分布,
已知条件下的概率分布,![]() 为e*和
为e*和![]() 的联合概率分布。
的联合概率分布。
(3)M-Step,在给定![]() 的条件下,计算
的条件下,计算![]() 新的极大似然(Maximum Likelihood, ML)或最大后验(Maximum A Posteriori, MAP)值。
新的极大似然(Maximum Likelihood, ML)或最大后验(Maximum A Posteriori, MAP)值。
在最大期望值算法中,以得到如下两种估计值:
ML
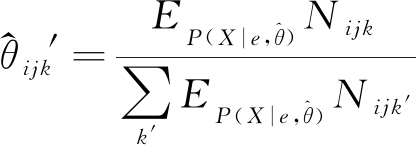
(5)
MAP
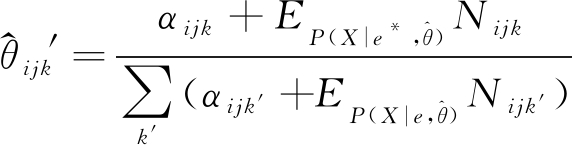
(6)
式中 αijk为狄利克雷参数,可以在E-Step和M-Step的迭代过程中得到。
E-Step用来计算事故数据中缺失值e*的最大期望统计量,M-Step根据上一步的计算结果,计算事故发生的条件下,各致因的各属性出现的概率值的新估计量。
本文EM算法的实现借助Netica软件来实现。Netica是贝叶斯网络学习软件,由于其强大的功能,友好的图形界面,且内置了参数学习的EM算法,已被广泛应用于不确定性管理领域,例如工程、医学和生态学[36]。
自动驾驶路测的事故机理,相比于人工驾驶既有共性,也有其特殊性。考虑到人工驾驶情况下事故数据较为充足,故本文采用人工驾驶情况下的网络参数作为先验知识,在此基础上采用最大期望算法,对自动驾驶路测情况下的网络参数进行渐进性估计,以突出自动驾驶路测的特点。
2.1.1 自动驾驶路测事故数据
截至2019年4月,美国加州机动车管理局(DMV)共收到并公布了148起自动驾驶汽车路测事故报告。基于该事故报告整理所得的是自动驾驶路测事故数据,包括事故基本信息和事故地点设施特征两部分。
事故基本信息直接从事故报告中提炼整理得到,包括事故日期、事故时间、事故地点、事故严重程度、驾驶模式、事故类型、天气、光照等。
事故地点设施特征是根据事故基本信息中的事故地点进行定位,获取谷歌街景图像进行人工判断得到,包括最大速度、是否为单行道、中央分隔带类型、车道数、坡度、曲率、交叉口类型等。图2以坡度、曲率为例,展示具体的判断案例。

图2 基于谷歌全景地图的道路特征参数判断案例(以曲率、坡度为例)
自动驾驶路测事故数据整理结果如表3所示。
表3 自动驾驶路测事故数据整理结果
2.1.2 人工驾驶事故数据
人工驾驶事故数据来源于美国国家公路交通安全管理局的事故报告采样系统(CRSS , The Crash Report Sampling System) 。CRSS涉及几乎所有的事故场景,从仅导致财产损失的轻微事故到导致死亡的严重事故均有覆盖。
从CRSS中导出其中2017年的所有事故数据,共有54969条。原始数据已被编码过,每一行对应一起事故,包含事故基本信息、车辆信息、驾驶员信息、事故前信息和人员信息五个部分。因为Netica软件处理数据量的限制,随机选取其中1000条数据进行处理。人工驾驶事故的致因影响程度分析结果是自动驾驶路测对比的基准,故选取和表3相同的变量数据,且对数据的属性进行一定的转换,以确保数据格式和自动驾驶路测事故数据相一致。
网络中所包含的变量及取值如表3所示。其中,设施因素包含交叉口类型、中央分隔带类型、车道数、坡度、曲率;交通因素包含最大速度;环境因素包含光照条件、天气;事故信息包括事故类型和严重程度。
根据前文所述的贝叶斯网络结构确定方法,结合专家知识,在具体影响因素层内,补充各因素间的因果关系:交叉口类型、中央分隔带类型和车道数,对最大速度有决定作用,事故类型对严重程度有决定作用。
最终确定网络结构如图3所示,其中CPT均为初始默认的等概率分布。
基于上述网络结构,在Netica中导入整理所得的事故信息表,利用Netica内置的EM算法进行参数学习。首先确定人工驾驶的网络参数,然后将其作为先验知识,在此基础上确定自动驾驶路测的网络参数。人工驾驶及自动驾驶路测的结果分别如图4(a)和4 (b)所示。
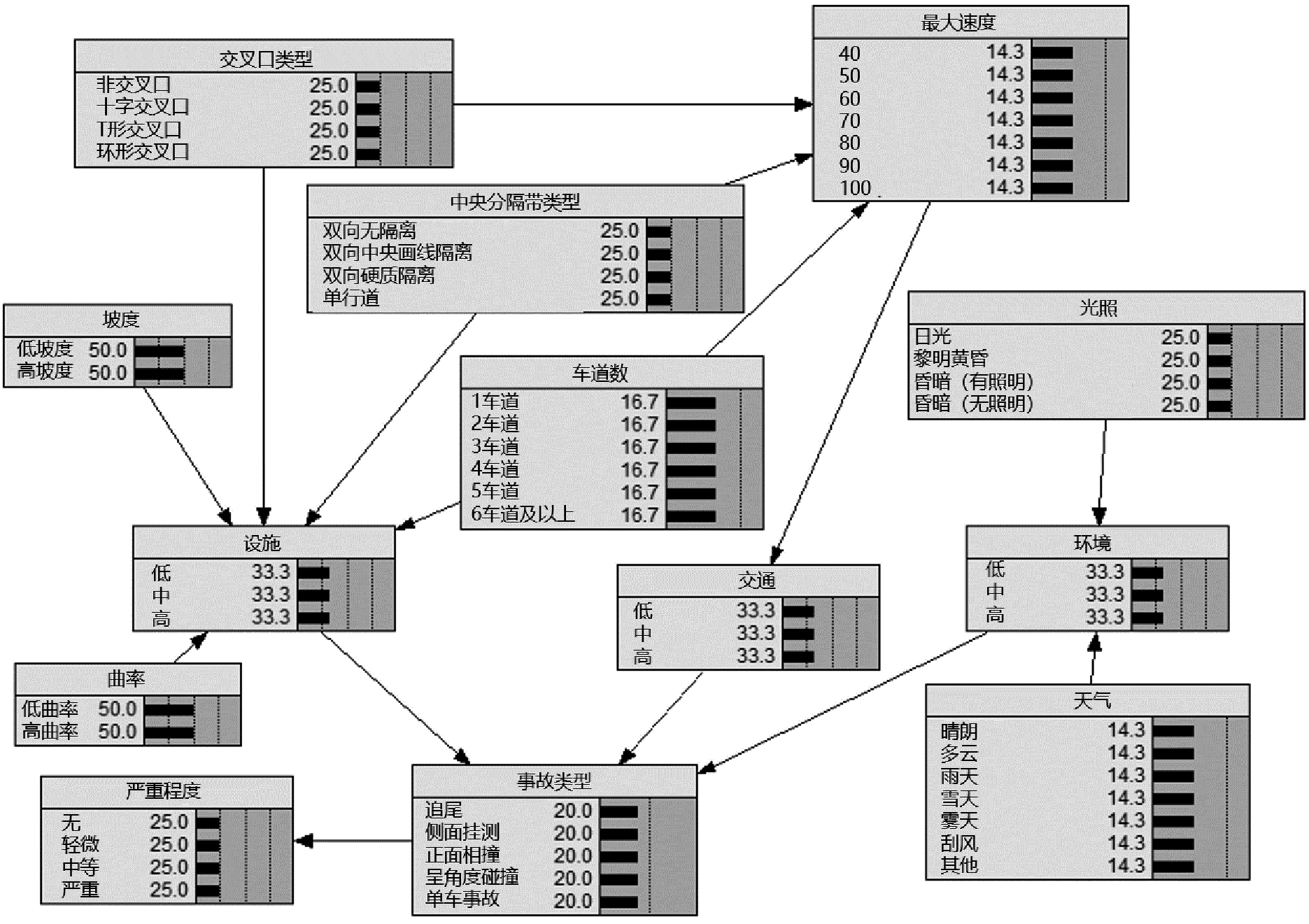
图3 贝叶斯网络结构
图4 人工驾驶/自动驾驶路测事故致因影响程度分析模型
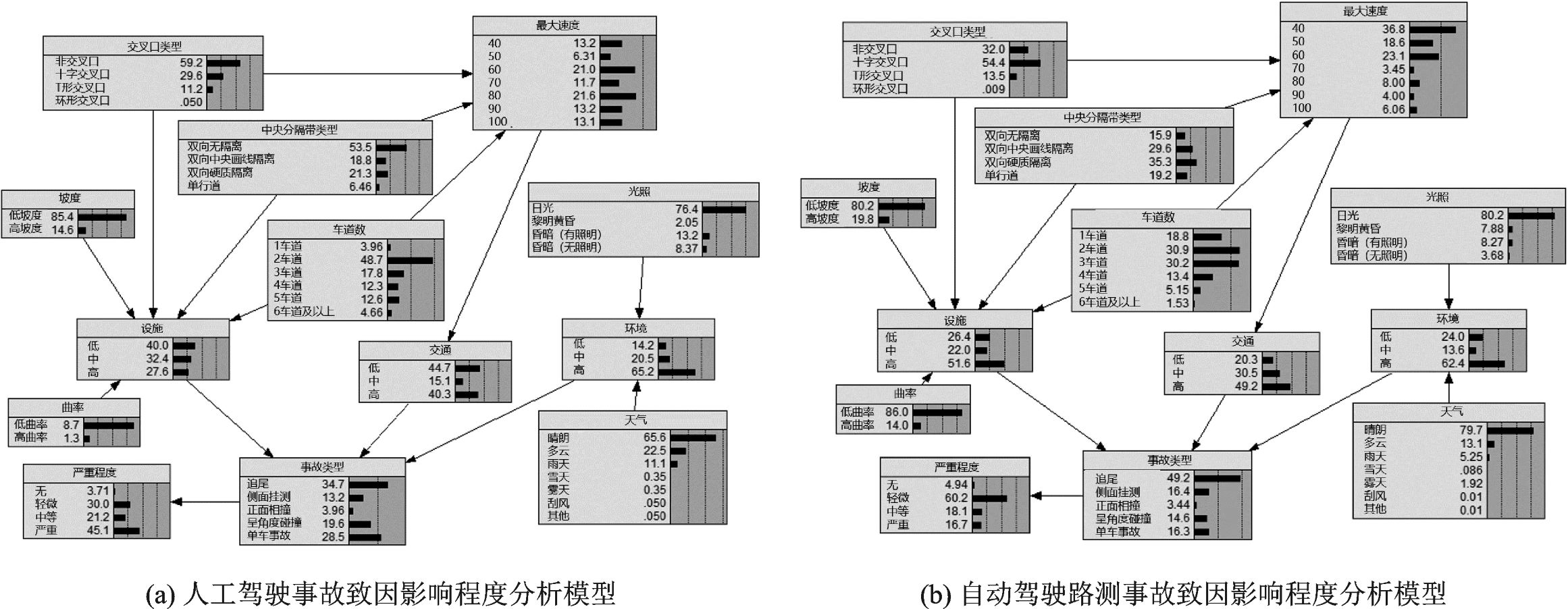
本文应用贝叶斯网络诊断推理的功能,分析在事故发生的条件下各解释变量的各个属性出现的概率,其概率值即为网络中各节点的参数值。对两种驾驶情况下事故发生在各影响因素的不同状态的概率列表进行对比,并将所得结论按照事故基本情况、道路几何因素、环境因素和交通因素分类总结,如表4和表5所示。
表4 自动驾驶路测与人工驾驶事故基本情况对比分析表
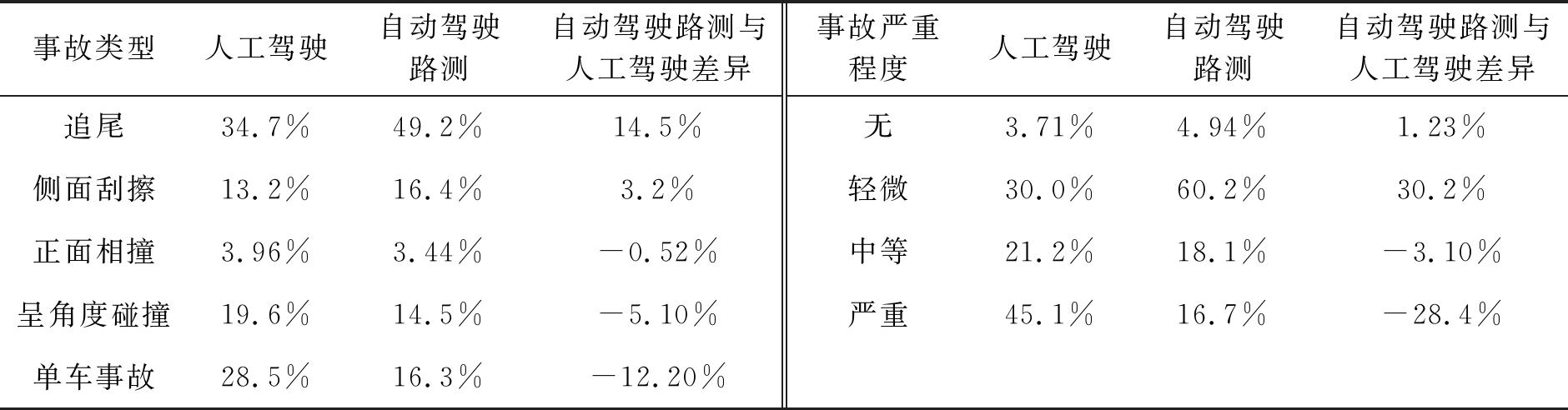
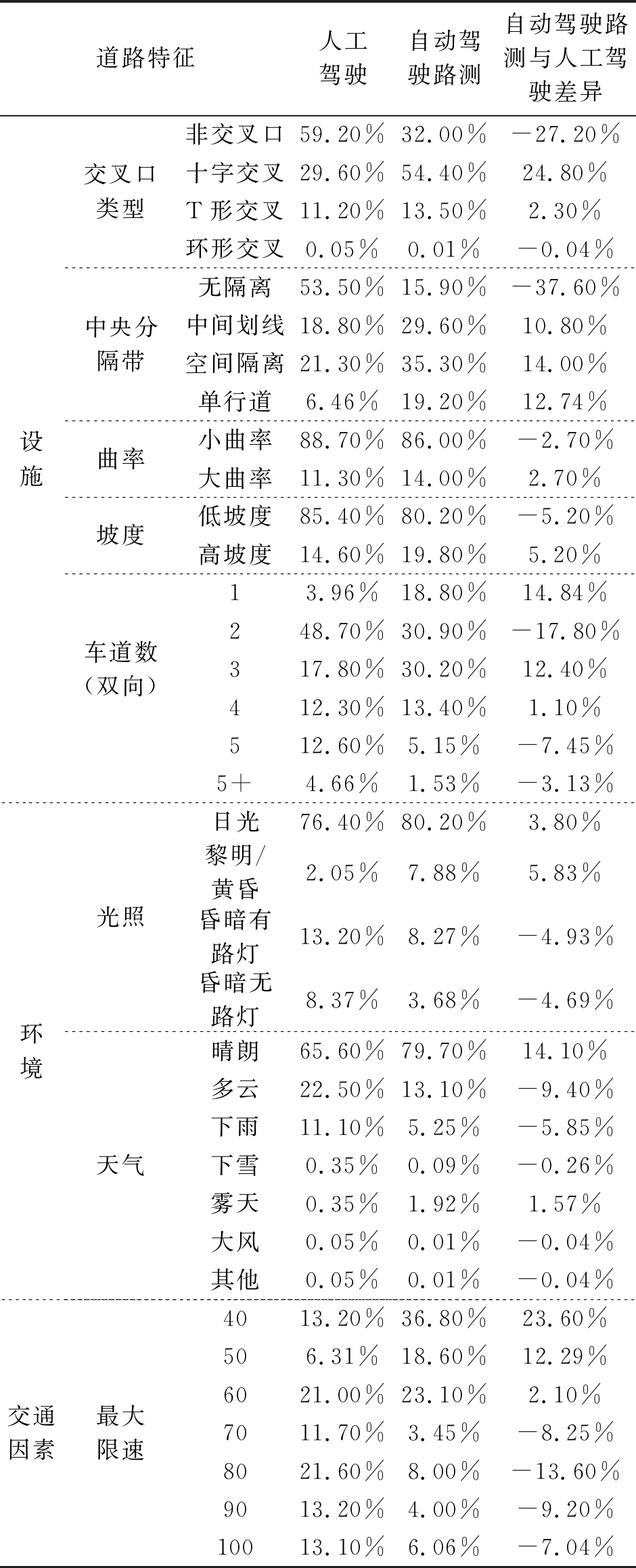
表5 自动驾驶路测与人工驾驶事故致因影响程度对比分析
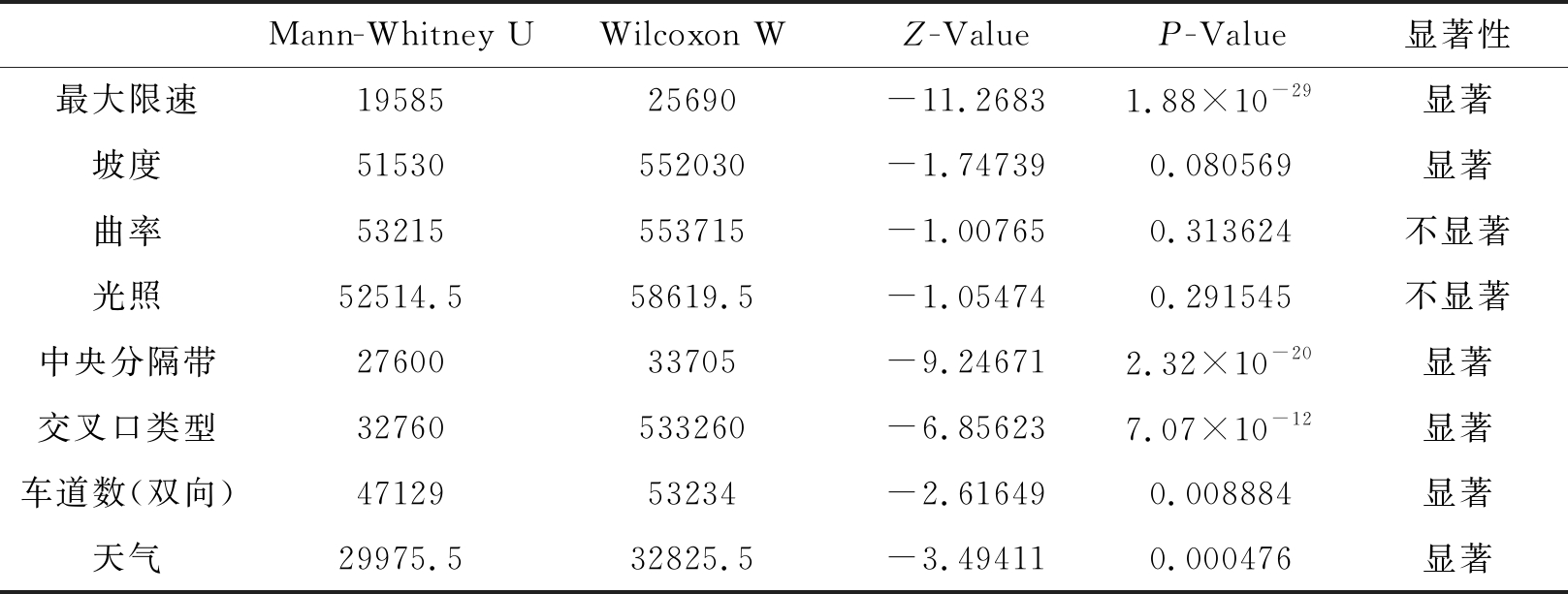
采用Mann-Whitney U检验方法,对两种驾驶模式下各事故致因影响程度差异进行显著性检验,结果如表6所示。
表4给出了自动驾驶路测事故基本情况的分析结果。表5给出了自动驾驶路测和人工驾驶事故致因影响程度对比分析结果。表6给出了两种驾驶模式下事故致因影响程度差异的显著性分析结果,其中最大限速、坡度、中央分隔带、交叉口类型、车道数(双向)、天气的影响均有显著差异,曲率、光照的影响差异相对不显著,约70%把握认为有差异,但考虑这两个致因会影响到自动驾驶的控制和感知系统,因此后文中仍保留相关分析。结果表明,自动驾驶路测事故致因影响程度,相对于人工驾驶的主要特点如下:
(1)事故基本情况
事故类型方面,自动驾驶路测更易发生追尾事故和侧面刮擦事故,比例分别上升14.5%和3.2%;正面相撞事故、呈角度碰撞事故以及单车事故比例均有所下降,其中单机动车事故比例下降12.2%。
事故严重程度方面,自动驾驶路测事故严重程度整体较低。轻微事故比例上升30.2%,严重事故比例下降28.4%。
事故类型和严重程度的影响具有一定的关联性:自动驾驶路测更易发生追尾和侧面刮擦事故,一般较为轻微,导致该驾驶情况下事故严重程度整体有所下降。
(2)道路设施因素
事故发生在单车道、双向三车道和双向四车道路段的概率上升,发生在其他路段的概率下降。平均来说,事故发生在双向四车道及以下路段的概率上升10.5%。这主要是因为车道数较少的路段一般等级较低,接入口相对较多,交通参与者冲突也多,因此道路环境也更加复杂,增加了自动驾驶风险。
事故发生在非交叉口的概率上升27.2%,发生在十字交叉口的概率上升24.8%,发生在T形交叉口的概率上升2.3%。交叉口的交通环境对于自动驾驶系统来说更加复杂,结合关于车道数的对比结论,表明自动驾驶路测在复杂交通环境下的适应性较差。
事故发生在高曲率和高坡度路段的概率分别上升2.7%和5.2%,说明不良横纵线形设计对自动驾驶路测安全性的影响更大。
中央为物理隔离的路段可有效降低人工驾驶情况下的事故概率。对于自动驾驶路测而言,数据分析表明这种效果则不明显。这和两种驾驶情况下的事故类型差异有一定的关系,自动驾驶路测中比例最高的追尾事故和侧面刮擦事故,与中央分隔带的关系均不大。
表6 自动驾驶路测与人工驾驶事故致因影响程度差异的显著性分析
(3)环境因素
事故发生在夜间的概率下降9.6%,发生在黄昏或黎明的概率上升5.8%,这和机器视觉的识别原理有关。光线的角度对机器视觉的性能有一定影响,逆光情况下其表现会有所下降,因此黄昏和黎明事故概率会上升。夜间机器视觉主要通过对比度来识别,表现优于人类驾驶员,故该条件下事故概率要更低。
事故发生在阴天和雨天的概率分别下降9.4%和5.9%,发生在雾天的概率上升1.6%。环境因素对两种驾驶情况的影响存在差异。
(4)交通因素
事故发生在限速60 km/h及以下路段的概率上升38.0%,其原因和车道数因素类似,低速路段等级较低,道路环境更加复杂。
本文通过对自动驾驶路测事故影响因素的梳理,结合父节点分离方法,确定了自动驾驶路测和人工驾驶事故致因影响程度分析的贝叶斯网络结构,利用EM算法并融合先验知识,完成了网络参数的学习,对比了人工驾驶和自动驾驶路测事故致因的影响程度。结果分析表明:自动驾驶路测与人工驾驶在事故致因影响程度的方面存在明显的差异性。事故类型方面,自动驾驶路测更易发生追尾事故和侧面刮擦事故;严重程度方面,轻微事故比例上升30.2%,严重事故比例下降28.4%,整体而言严重程度有所下降;道路设施环境和交通因素方面,事故发生在双向四车道及以下路段的概率上升10.5%,发生在十字交叉口的概率上升24.8%,发生在非交叉口的概率下降27.2%,发生在限速60 km/h及以下路段的概率上升38.0%,说明自动驾驶路测在复杂交通环境下的适应性较差;环境因素方面,事故发生在黄昏、黎明时分的概率上升5.8%,说明逆光下自动驾驶路测安全风险隐患高。
后续研究将进一步扩大自动驾驶路测事故数据规模,并开展基于我国相关事故数据的模型验证,同时利用专家知识与实际数据融合的方法确定和优化贝叶斯网络结构,进一步提升结论的合理性和适用性。
[1] 周 锐, 李 力.智能驾驶测试面临的挑战[J]. 人工智能, 2018(6): 59-70.
[2] 韩梦霄.把命交给自动驾驶,你敢吗?[J]. 人民交通, 2019,(12): 31-5.
[3] 金 宇,王晓峰. 基于贝叶斯网络的交通事故原因分析[J]. 现代计算机(专业版), 2018(24):7-10.
[4] 李 康. 基于贝叶斯网络的高速公路交通事故研究[D]. 北京:北京交通大学,2017.
[5] 卢 瑶.山区高速公路交通事故的贝叶斯网络模型诊断及推理研究[D]. 武汉:华中科技大学, 2019.
[6] 童璐璐.基于贝叶斯网络的高速公路交通事故严重程度预测研究[D]. 北京:北京交通大学, 2018.
[7] 杨成龙.城市道路交通事故致因分析及管理研究[J]. 商,2016,(22): 279.
[8] 钟珊珊.道路交通安全影响因素关系研究[D]. 武汉:武汉理工大学, 2017.
[9] 周菲菲.基于贝叶斯网络城市道路交通事故成因分析[D]. 长沙:湖南师范大学,2017.
[10] 丁雨蕾.重特大交通事故特征及影响因素分析[D]. 南京:东南大学, 2016.
[11] 袁 黎,于俊俊,吴梦倩,等.基于贝叶斯网络的双车道公路风险性分析[J]. 公路工程, 2016, 41(2): 99-103.
[12] 赵金宝, 邓 卫, 王 建.基于贝叶斯网络的城市道路交通事故分析[J].东南大学学报(自然科学版),2011,41(6):1300-1306.,
[13] 胡立伟, 李耀平.典型交通设施对道路交通事故致因影响分析[J].武汉理工大学学报(交通科学与工程版),2014, 38(1):98-102.
[14] 胡顺峰. 山区高速公路隧道群交通事故特征及致因机理分析[J]. 公路, 2016,61(5): 134-138.
[15] Holubowycz O T. Age, sex, and blood alcohol concentration of killed and injured pedestrians[J].Accident Analysis & Prevention,1995,27(3):417-22.
[16] Lord D, Washington S P, Ivan J N. Poisson, Poisson-gamma and zero-inflated regression models of motor vehicle crashes: balancing statistical fit and theory[J].Accident Analysis & Prevention,2005,37(1):35-46.
[17] 陈 异, 戴 琳, 寇 鹏.零膨胀泊松回归模型及其在交通事故中的应用[J]. 计算机技术与发展,2013, 23(10): 163-166.
[18] 马 聪, 张生瑞, 马壮林, 等.高速公路交通事故非线性负二项预测模型[J]. 中国公路学报,2018, 31(11): 176-185.
[19] 张祎祎.基于改进负二项回归模型的高速公路交通事故起数预测方法研究[D]. 西安: 长安大学, 2017.
[20] 陆 欢, 戢晓峰, 杨文臣, 等.高原山区公路环境下交通事故形态致因分析[J]. 中国安全科学学报,2019, 29(5): 44-49.
[21] 曹 堉, 王 成, 杨岳铭, 等. 基于贝叶斯网络的城市道路交通拥堵多原因自动实时识别[J].公路交通科技,2020,37(11):89-97.
[22] 许洪国, 张慧永, 宗 芳.交通事故致因分析的贝叶斯网络建模[J].吉林大学学报(工学版),2011,41(S1):89-94.
[23] Favarò F M, Nader N, Eurich S O, et al. Examining accident reports involving autonomous vehicles in California[J].PLoS ONE,2017,12(9):e0184952.
[24] Boggs A M, Wali B, Khattak A J. Exploratory analysis of automated vehicle crashes in California: A text analytics & hierarchical Bayesian heterogeneity-based approach[J]. Accident Analysis & Prevention, 2020, 135: 105354.
[25] Wang S, Li Z. Exploring causes and effects of automated vehicle disengagement using statistical modeling and classification tree based on field test data[J].Accident Analysis & Prevention,2019,129:44-54.
[26] Ye W, Wang C, Chen F, et al. Approaching autonomous driving with cautious optimism: analysis of road traffic injuries involving autonomous vehicles based on field test data[J]. Injury Prevention, 2020,27(1):42-47.
[27] Das S, Dutta A, Tsapakis I. Automated vehicle collisions in California: Applying Bayesian latent class model[J]. IATSS Research, 2020,44(4):300-308.
[28] 熊晓夏,陈 龙,梁 军,等. 基于贝叶斯网络模型的道路交通事故链生成与演化研究[J].公路交通科技,2018,35(5):99-107.
[29] von Waldow U, Röhrbein F. Structure learning in Bayesian networks with parent divorcing[C]. EuroAsianPacific Joint Conference on Cognitive Science, Torino, Italy, 2015:146-151.
[30] Rohrbein F, Eggert J, Korner E. Child-friendly divorcing: Incremental hierarchy learning in Bayesian networks[C]. International Joint Conference on Neural Networks, Atlanta,USA,2009,1:2711-2716.
[31] Neapolitan R E. Learning Bayesian Networks[M]. Prentice-Hall Inc., NJ,USA, 2004.
[32] OLESEN K G, KJAERULFF U, JENSEN F, et al. A munin network for the median nerve—a case study on loops[J]. Applied Artificial Intelligence an International Journal. 1989, 3(2-3): 385-403.
[33] Demissie S, Lavelly M P, Horton N J, et al. Bias due to missing exposure data using complete—case analysis in the proportional hazards regression model[J]. Statistics in Medicine. 2003, 22(4): 545-57.
[34] Pilla R S, Lindsay B G. Alternative EM methods for nonparametric finite mixture models[J]. Biometrika,2001, 88(2): 535-50.
[35] ZOU X, YUE W L.A Bayesian network approach to causation analysis of road accidents using netica[J].Journal of Advanced Transportation,2017:2528481.
[36] Mcheick H, Nasser H, Dbouk M, et al. Stroke prediction context-aware health care system[C]. Proceedings of IEEE First International Conference on Connected Health: Applications, Systems and Engineering Technologies (CHASE), Washington DC, USA, 2016: 30-35.