引 言

随着中国高层及超高层建筑的蓬勃发展和城市地下空间的大规模开发，基坑开挖的深度及规模急剧增大，施工工艺及周边环境随之日益复杂，因此基坑施工及设计的难度越来越大，深基坑的安全性越发受到重视。目前传统深基坑失稳风险的评估方法是定性的，如专家问卷调查法、加权平均法、风险概率及后果综合评价法等，如：徐传华等[1]利用模糊综合评判法对地下工程的围岩稳定性进行了判定；兰守奇等[2]等基于模糊理论对深基坑施工期的风险进行了评估；张驰等[3]基于模糊数学的相关理论对深基坑施工环境的影响进行了评价；边亦海等[4]利用风险概率与风险后果的组合标准研究了基坑工程的风险大小和水平。由于影响基坑安全性的因素较多，且相互联系，难以用一个定量的指标去表征[5]。虽然传统评价方法在一定程度上反映工程风险的水平，但基于专家打分法所获得的风险事件发生概率无法体现各风险因素的综合作用和相互影响，致使评价结果与实际偏差较大，不能客观真实地反映深基坑的危险安全程度。因此有必要引入一种新的计算风险概率与风险后果的方法，从而使得评价结果更具有合理性和可操作性。

为此，本文在深入分析基坑失稳风险综合模型的基础上，针对土层物理参数及周边环境的不确定性，引入了模糊概率统计法对基坑失稳概率进行研究，采用熵理论对基坑失稳风险后果进行改进，从而建立基于模糊理论及熵理论的基坑失稳风险综合评价方法。

1 基坑失稳风险综合评价方法

本文拟建立的基坑失稳风险综合评价方法主要包括3个方面的内容，即基坑失稳风险综合分析模型、模糊概率评价方法以及基于信息熵理论的风险后果专家调查分析方法，下面将作详细介绍。

1.1 基坑失稳风险综合分析模型

分析悬臂支护结构下基坑失稳风险时，应考虑主要不确定因素，而忽略那些确定的或次要因素，因此，本文在总结现有研究成果[6-8]基础上，将基坑失稳风险分解成图1所示的4个风险事件及主要风险因素。

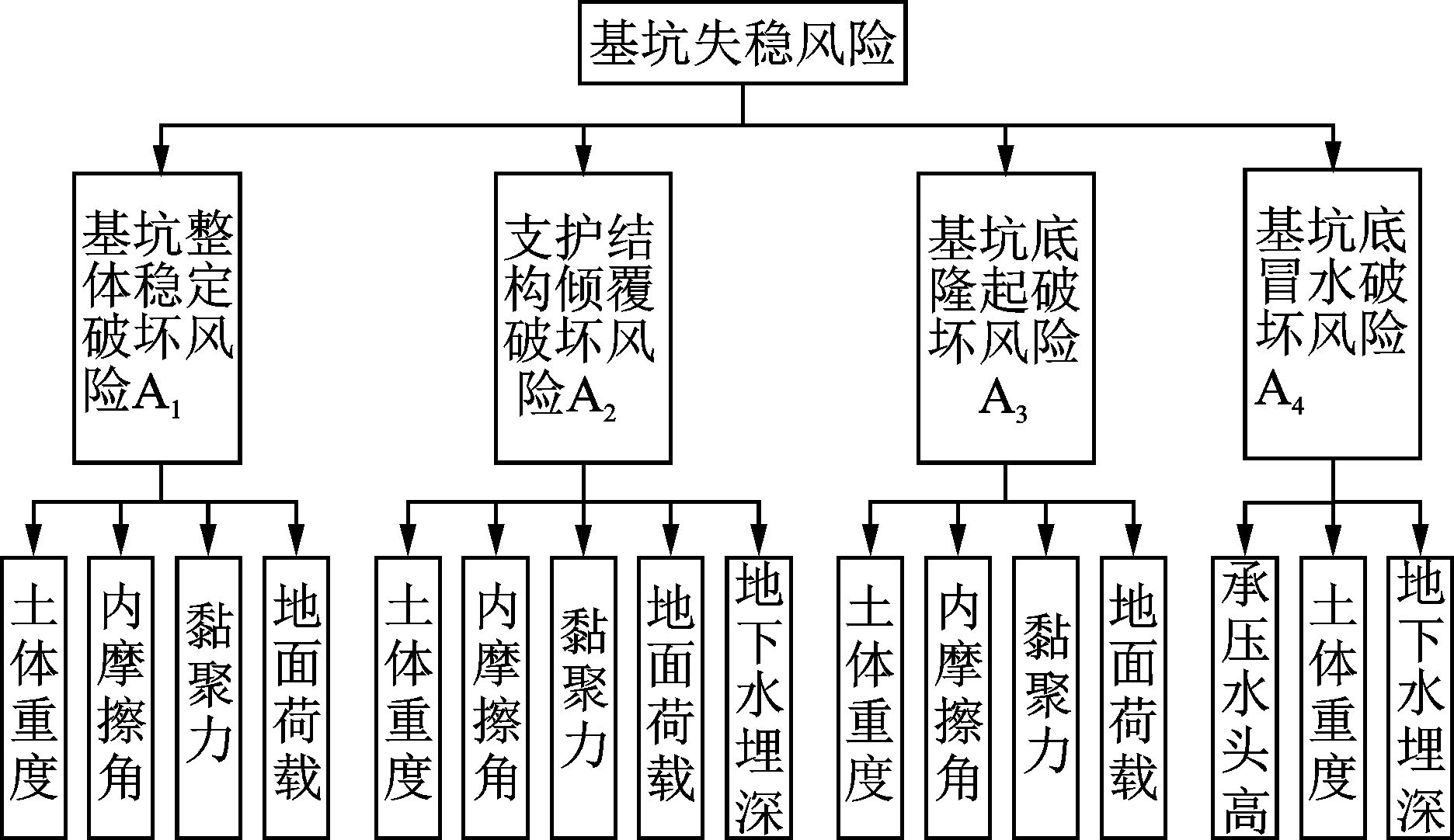
图1 基坑失稳风险事件及风险因素

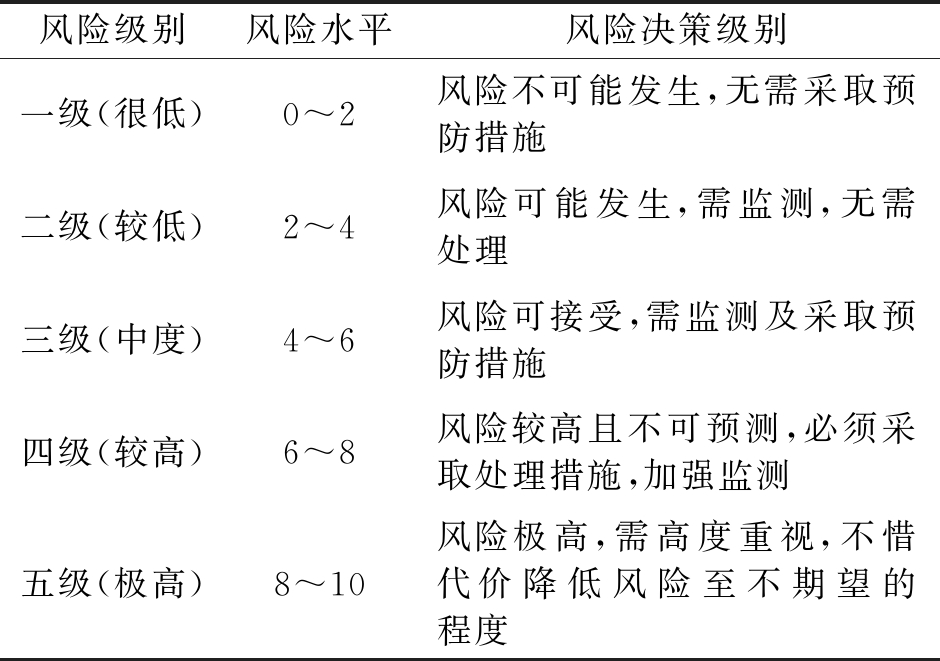
风险综合评价模型的建立是基坑失稳风险评价的前提。而基坑失稳总体风险水平的评价标准应综合考虑风险概率及风险后果的影响(见表1)，因此，综合考虑4个风险事件对悬臂支护结构基坑失稳总体风险水平的影响，构建基坑失稳风险综合评价模型

(1)

式中 Ci为基坑失稳的总体风险水平，wi(i=1,2,3,4)分别为4个风险事件(A1,A2,A3,A4)的权重，pi为第i个风险事件的发生概率，Ui为第i个风险事情发生后的风险后果，Mi=wiUi为风险事件Ai综合考虑风险事件权重及风险后果后的风险水平。

对于基坑失稳的总体风险水平的权重选取采用常用的层次分析法(AHP)法，首先根据两两风险事件的重要程度采用1～9的标度赋予相应的权重，从而构建两两比较的构造判别矩阵然后根据分层总和法求出4个风险事件的权重wi，风险事件(A1,A2,A3,A4)的权重值wi分别为：0.3570，0.3912，0.1043，0.1475。

1.2 基坑失稳风险的模糊概率评判方法

由于基坑失稳的风险受多种因素影响，且各因素具有很强地不确定性和复杂性，致使基坑失稳风险问题表征为多因素的复杂动态体系。基坑失稳风险的评价方法较多，由于基坑失稳风险集模糊性与随机性为一体，而层次分析法及熵权法多进行定量分析，因此，采用模糊概率评判方法来评价基坑失稳发生概率较为合理[9]。

表1 风险级别及决策

(1)模糊概率理论

将普通权重p(ui)换成语言概率πi，则可得到模糊事件的模糊权重。即设A为模糊事件，p(ui)=πi，则一个事件的模糊概率为

p(Aj)=Aj(u1)π1+Aj(u2)π2+…+Aj(un)πn

(2)

(2)基坑失稳风险综合评判模型

基于模糊概率理论获得基坑失稳风险评判步骤：

①确定基坑失稳风险的主要影响因素ui，建立评价影响因子集即

(3)

②基于主要影响因子ui与基坑失稳风险等级Aj的模糊关系，确定隶属函数Aj(ui)，即确定了Aj是论域U上的一个模糊子集，使得

Aj=Aj(u1)u1+Aj(u2)u2+…+Aj(un)un

(4)

③分析主要影响因子ui的模糊数(模糊权重)πi(i=1,2,…,n)，即把模糊权重看成模糊数

πi=βi,1λi,1+…+βi,mλi,m+λi0+

βi,m+1λi,m+1+…+βi,2mλi,2m

(5)

将πi归一化后可得：式中：一般可取为0.5，0.6，0.7，0.8，0.9中的一个值；λij(j=1,2,…,2m)的值可由λi0值来合理确定。

④根据模糊事件的语言概率公式(2)，利用式归一化处理即可得到基坑失稳风险等级Aj的模糊概率p(Aj)。则第j个风险评价等级的任一稳定等级第i个隶属度ai即为Aj(ui)。

(3)隶属函数的确定

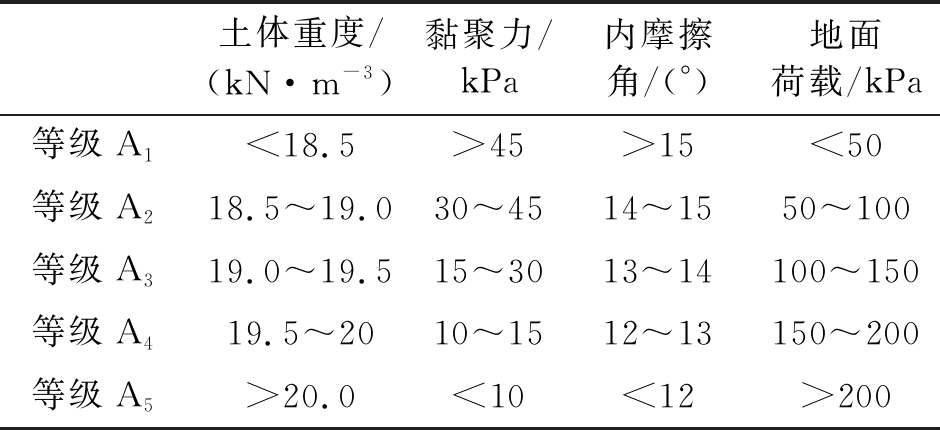
由于基坑失稳风险受4个因素所控制，下面仅以基坑整体破坏风险为例，按照危险程度通常将破坏风险分为风险不可能(A1)、风险很少发生(A2)、风险偶尔发生(A3)、风险可能发生(A4)、风险频繁发生(A5)这5个等级，其风险各评价因子的分级标准如表2所示。

表2 风险各评价因子的分级标准

利用隶属函数来建立主要影响因子ui(i=1,2,3,4)与基坑失稳风险等级Aj(j=1,2,3,4,5)之间的模糊关系，目前常见隶属函数有：线性型(三角形分布、梯形分布)和非线性型(正态分布、岭形分布)等。本文根据各因子数据之间的分布特征，综合考虑认为采用梯形隶属函数是比较合理的。而影响因子可分为递减型和递增型两类；对于递增型影响因子(i=1,4)，其隶属函数表达式为：

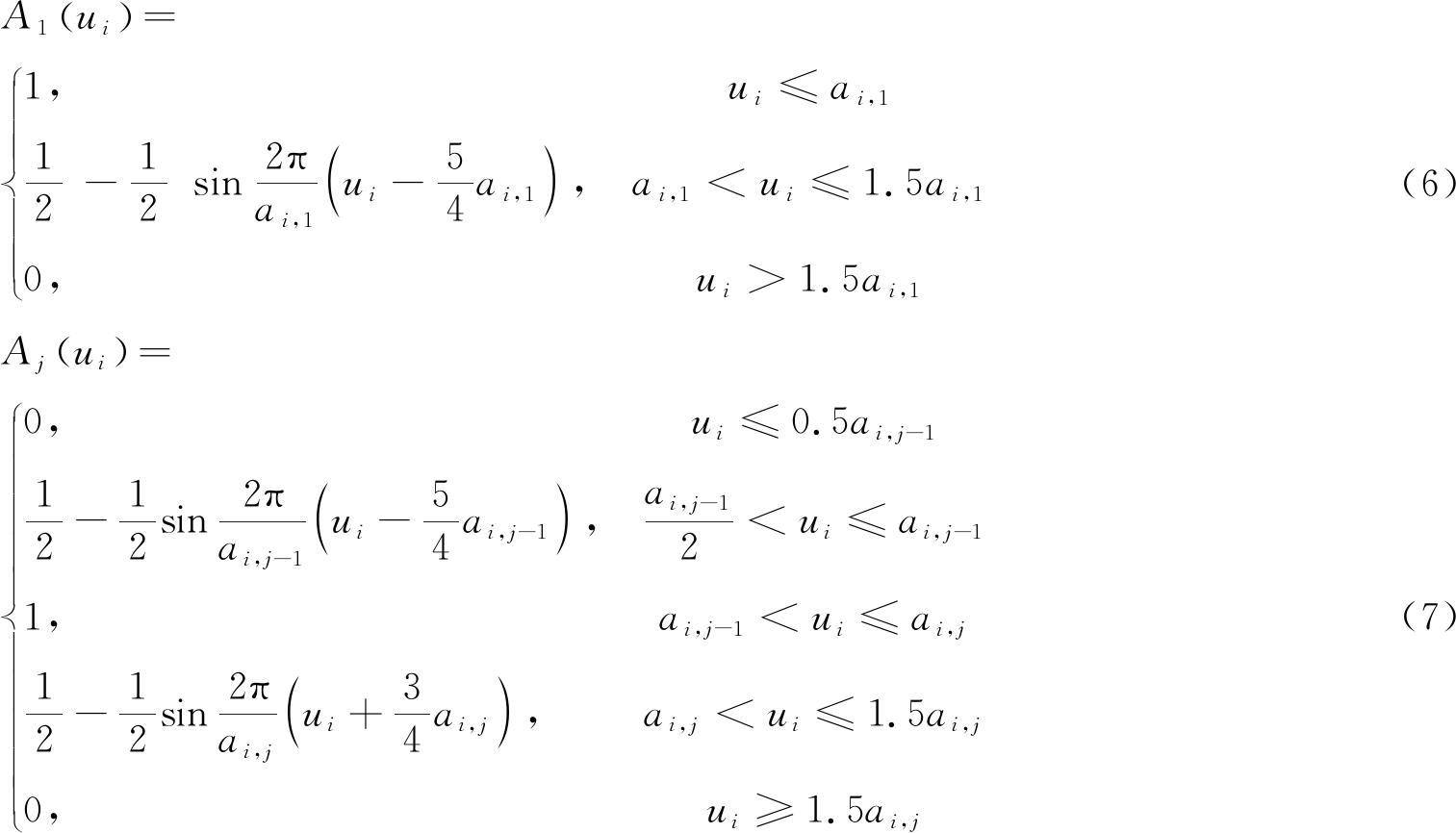
(8)

式中 j=2,3,4；ai,k为评价指标因子ui的等级划分标准。

对于递减型影响因子(i=2,3)，可采用隶属函数式(6)的转化式来确定评价指标因子，其各评价等级的隶属函数表达式为

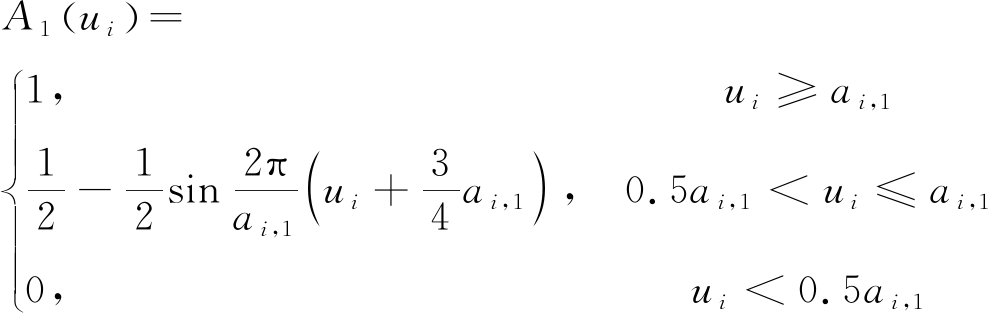
(9)

式(7)的隶属函数表达式应改为

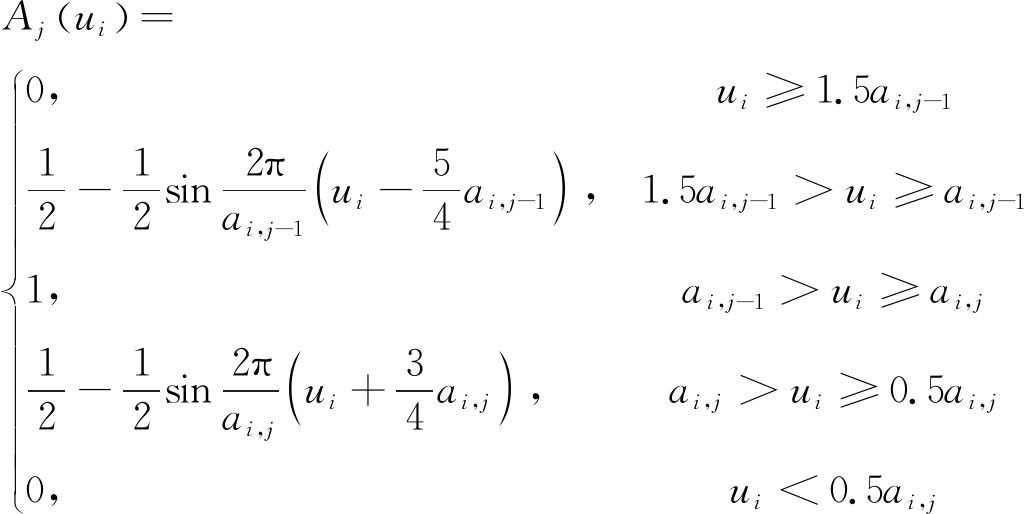
(10)

式(8)的隶属函数表达式应改为

(11)

(4)模糊权重的确定

在模糊综合评判法对影响对象进行概率评判时，其评价指标因子的权重取值将影响评判结果，现有权重确定方法往往将权重作为一定值，而实际上权重具有模糊性，因此应采用模糊权重的方法来进行考虑。

将分层总和法得到的基坑整体稳定破坏风险中土体重度、黏聚力、摩擦角、地面荷载的权重值归一化后转化为λi,0，使得∑λi,0=1。因此，它们建议的相对权重值分别为

λ0=(0.236,0.295,0.218,0.251)

在相对权重的基础上，引入模糊概率理论，用模糊权重来修正各评价影响因子中的相对权重，结果为：

π1=β1,1·0.136+1·0.236+β1,2·0.336，

π2=β2,1·0.195+1·0.295+β2,2·0.395，

π3=β3,1·0.118+1·0.218+β3,2·0.318，

π4=β4,1·0.151+1·0.251+β4,2·0.351

式中 可建议均取为βi,1=0.6，βi,2=0.7，可得到模糊权重值归一化后的结果为：

以上分析表明，基坑整体破坏风险的权重具有双重性，即模糊性与动态性。表明模糊概率理论所获得的模糊权重所反映的权重取值的合理性。

1.3 基坑失稳风险后果的计算方法

基坑风险后果的种类繁多，包括经济损失、工期损失、人员损失等多方面，且风险后果具有很强的不确定性，现阶段采用较为粗糙的专家调查法预估的风险后果往往也差异较大，即不同专家的决策水平(评价结果的可信度)并不相同，因此，有必要针对现有专家调查法存在的问题展开深入研究，建立一种能有效反映专家决策水平的风险后果评价方法。

由于信息熵可以用来度量不同指标的信息效用值，且可消除各指标权重计算的人为干扰，使评价结果更符合实际[10]，因此采用熵值对敏感度样本方案的集合进行权重化处理。其具体实施过程如下：

(1)构建m个专家对n个风险事情的风险后果评价矩阵R=(Rij)m×4。式中Rij为第i个专家对第j个风险事件的风险综合评分值。Rij可按下式计算

Rij=0.4r1ij+0.2r2ij+0.4r3ij

(12)

式中 r1ij，r2ij，r3ij分别为专家对每个风险事件可能出现的经济损失、工期损失和人员损失的评分值。

(2)将上述风险后果评价矩阵进行归一化，即

xij=(Rij-Rmin)/(Rmax-Rmin)

(13)

式中 Rmax，Rmin分别为不同专家对同一风险事情的风险后果综合评分值的最大值和最小值。

根据信息熵的定义，确定风险后果熵为

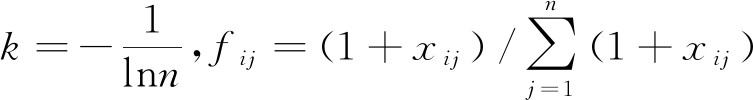
(14)

由上式可见，熵权Hi越小，则该指标值的变异程度越大,在评价中的作用越大;反之，熵值Hi越大，则该指标值的变异程度越小，在评价中的作用越小。

(4)显然，决策水平越高的专家所给的评价结果应赋予越大的权重，故专家Si的自身权重E为

(15)

根据上式，得到了不同专家对不同风险事件的风险后果综合评分熵值化后的结果即风险结果熵，因此，考虑专家评价水平的风险后果评分向量为

Ui=EA

(16)

式中 Ui=(U1,U2,U3,U4)为4个风险事件的风险评价向量，E=(E1,E2,E3,E4)为专家自身权重向量，A=(rij)4×4为基坑风险后果评价矩阵。

2 工程实例分析

2.1 工程概况

为验证本文计算方法的可行性，将其应用于合肥花园宾馆深基坑失稳风险评估中。该大厦基坑开挖深度达H=22 m，地面均布垂直荷载q=80 kPa，地下水位为地面以下8.5 m，承压水头高为8.5 m，采用悬臂式支护桩结构，基坑各土层分布及物理力学性质如表3所示。

表3 基坑各土层情况

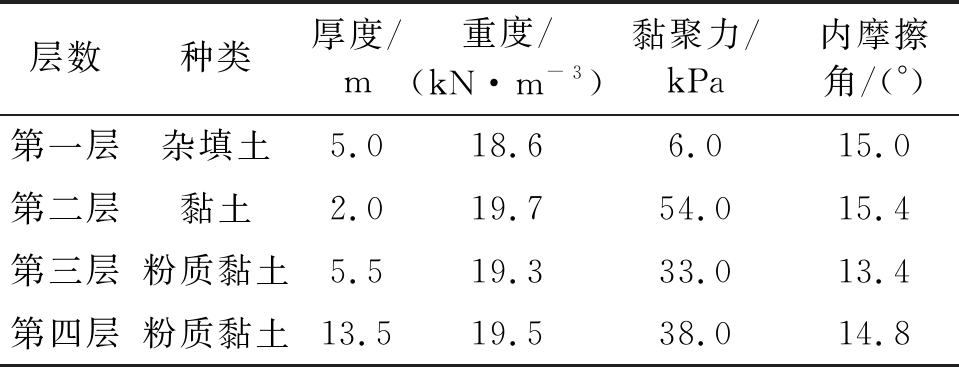
各层指标变异性可忽略，根据厚度加权平均法可求得土体的重度为重度γ1=19.3 kN/m3，黏聚力c=32.0 kPa，内摩擦角φ=14.6°。

2.2 分析过程及结果

采用本文方法对该基坑失稳风险进行评估，其具体过程如下：

(1)计算风险概率

首先，由隶属函数公式(6)～(11)计算主要影响因子对于基坑各稳定等级的隶属度见表4。

表4 主要影响因子在基坑各稳定等级的隶属度

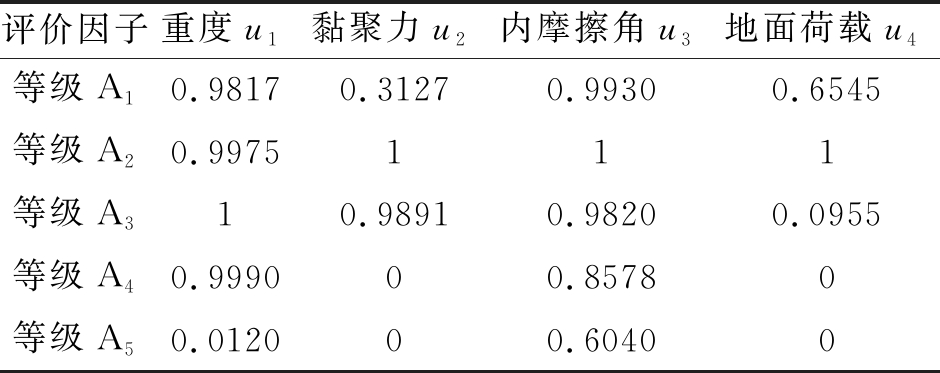
由语言概率公式可得各稳定等级Aj的模糊概率p(Aj)=(1.483,0.999,0.767,0.426,0.137)，进一步可得到归一化后的信息集中值为

同理可获得支护结构倾覆破坏风险、基坑底隆起破坏风险、基坑底冒水破坏风险的模糊概率归一化后的结果：(0.192,0.253,0.186,0.183,0.186)，(0.143,0.192,0.288,0.275,0.102)，(0.124,0.226,0.312,0.185,0.172)。

(2)计算风险后果

a)确定风险后果评价矩阵。将4个专家对4个风险事件的风险后果给出了评分，由式(12)得到风险后果的评价矩阵A=(rij)4×4，如表5所示。

表5 基坑失稳风险损失评分值

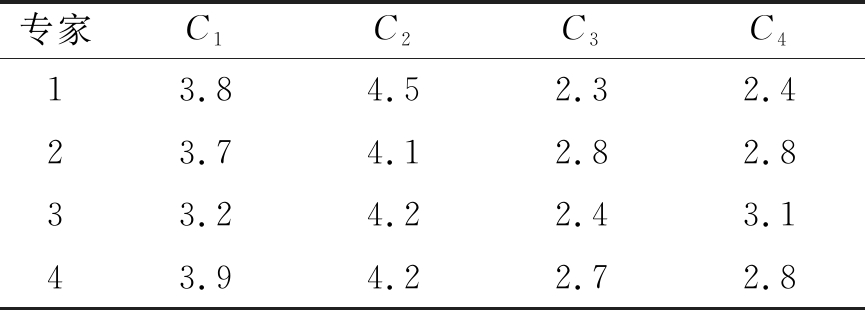
b)由式(13)和式(14)可求得4个专家的风险评价熵值Hi分别为(0.4846,0.4981,0.4894,0.4914)，再由式(15)可获得4个专家的自身权重E分别为(0.4215,0.0520,0.2898,0.2367)。

c)根据4个专家的自身权重对风险后果评价矩阵A=(rij)4×4进行修正，由式(16)可获得基坑失稳风险的最终评分值向量为Ui=(3.644,4.321,2.449,2.718)。

d)Ai综合考虑风险事件权重及风险后果后的风险水平为：Mi=wiUi=(1.301,1.691,0.256,0.401)

e)计算基坑失稳的总体风险Ci。将计算得到Mi和风险事件发生概率pi代入式(1)计算得到Ci

(17)

则基坑失稳的总体风险C=∑Ci=3.64，由表1可知该基坑的失稳总体风险为二级，风险可能发生，需对基坑进行监测，但无需采取风险处理措施。由于支护结构倾覆破坏的风险水平达到1.691，因此，在工程施工时应重点对支护结构进行监测。

实际工程表明该基坑的支护结构比较安全，这与本文的分析结果相一致，说明该方法能较好地反映工程实际情况，从而论证了该方法的合理性与可行性。

3 结 论

本文在现有风险评价理论的基础上引入模糊概率评判方法和信息熵理论，采用风险概率与风险后果的组合标准对基坑失稳风险水平进行深入研究，得出有益结论：

(1)基于模糊概率理论及信息熵理论，建立了综合考虑风险概率及风险后果的基坑失稳风险综合评价方法。

(2)采用模糊概率评判方法确定风险概率时，由于引入模糊概率理论对相对权重进行修正，使得评价结果更符合工程实际。

(3)采用信息熵理论来度量不同指标的信息效用值，可真实反映专家评价的水平，使得评价结果更符合工程实际。

参考文献：

[1] 许传华, 任青文. 地下工程围岩稳定性的模糊综合评判法[J]. 岩石力学与工程学报,2004,23(11):1852-1855.

[2] 兰守奇, 张庆贺. 基于模糊理论的深基坑施工期风险评估[J].岩土工程学报, 2009,31(4):648-652.

[3] 张驰, 黄广龙. 深基坑施工环境影响的模糊风险分析[J].岩土工程学报, 2013,32(1):2669-2675.

[4] 边亦海, 黄宏伟. SMW工法支护结构失效概率的模糊事故树分析[J].岩土工程学报, 2006,28(5):664-668.

[5] 中华人民共和国建设部.地铁及地下工程建设风险管理指南[M]. 北京: 中国建筑工业出版社, 2007.

[6] CHO H N, CHOI HH, KIM Y B. A risk assessment methodology for incorporating uncertainties using fuzzy concepts[J]. Journal of Reliability Engineering and System Safety, 2002, 78(2): 173-183.

[7] 毛儒. 隧道工程风险评估[J]. 隧道建设, 2003,23(2):1-3.

[8] 张瀚，陈建康，高策，等. 基于熵权集的大坝分部位动态健康评价方法研究[J]. 四川大学学报(工程科学版), 2014, 46(6): 56-62.

[9] 廖瑛. 基坑支护结构的稳定可靠度研究[J]. 工业建筑, 2004,34(1):54-56.

[10] 王广月. 深基坑支护决策的信息熵模糊层次分析模型[J].岩土力学, 2004,25(12):737-739.

Comprehensive evaluation method of instability risk for foundation pit

CHENG Tao1,2, SUN Xuejun1,2, LI Yougui2, LIU Shunqing3, YANG Zonglin2

(1.Anhui Road & Bridge Engineering Group Co. Ltd., Hefei 230031, China; 2.Anhui Construction Engineering Group Co. Ltd., Hefei 230031, China; 3.Jiangsu University of Science and Technology, Zhenjiang 212005, China)

Abstract： Foundation pit engineering has many economic and technological risks in the construction process, including: stability of foundation pit retaining structure damage risk, overturning failure risk, the bottom of the foundation pit uplift failure risk, pit bottom water damage risk, it is difficult to use a certain value to identify them. Therefore, weight is modified based on the theory of fuzzy probability, membership size of the main influencing factors is obtained according to the appropriate membership functions, the fuzzy probability of the stable level is gained; the evaluation method for the risk consequence is formulated based on information entropy theory; the overall risk of instability of foundation pit is obtained from the risk events weight, the risk consequences of risk events, the probability of risk events, for which is based on fuzzy theory and entropy theory of foundation pit risk comprehensive evaluation method. Finally, the risk of whole instability for foundation pit of Hefei Garden Hotel by this method is 3.64, the risk level is level 2, and foundation pit must be monitored, but no need for risk treatment measures.

Key words： foundation pit engineering; risk assessment; fuzzy theory; entropy theory

中图分类号：TU433; TU473.2

文献标志码：A

文章编号:2097-017X(2021)03-0017-06

*收稿日期： 2021-06-07

基金项目：住建部2015年科学技术项目计划(2015-K4-027)；安徽省博士后基金资助项目(2016B085)

第一作者简介： 程 涛(1983-)，男，博士，高级工程师。研究方向：道路与桥梁工程。